已知函数 ,其中
,其中 为大于零的常数,
为大于零的常数,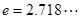 ,函数
,函数 的图像与坐标轴交点处的切线为
的图像与坐标轴交点处的切线为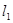 ,函数
,函数 的图像与直线
的图像与直线 交点处的切线为
交点处的切线为 ,且
,且 .
.
(I)若在闭区间 上存在
上存在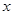 使不等式
使不等式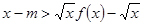 成立,求实数
成立,求实数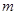 的取值范围;
的取值范围;
(II)对于函数 和
和 公共定义域内的任意实数
公共定义域内的任意实数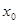 ,我们把
,我们把 的值称为两函数在
的值称为两函数在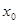 处的偏差.求证:函数
处的偏差.求证:函数 和
和 在其公共定义域内的所有偏差都大于2.
在其公共定义域内的所有偏差都大于2.
推荐套卷
已知函数 ,其中
,其中 为大于零的常数,
为大于零的常数,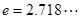 ,函数
,函数 的图像与坐标轴交点处的切线为
的图像与坐标轴交点处的切线为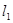 ,函数
,函数 的图像与直线
的图像与直线 交点处的切线为
交点处的切线为 ,且
,且 .
.
(I)若在闭区间 上存在
上存在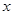 使不等式
使不等式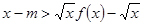 成立,求实数
成立,求实数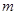 的取值范围;
的取值范围;
(II)对于函数 和
和 公共定义域内的任意实数
公共定义域内的任意实数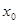 ,我们把
,我们把 的值称为两函数在
的值称为两函数在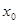 处的偏差.求证:函数
处的偏差.求证:函数 和
和 在其公共定义域内的所有偏差都大于2.
在其公共定义域内的所有偏差都大于2.