如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数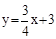 的图象与y轴的交点,点B在二次函数
的图象与y轴的交点,点B在二次函数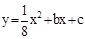 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.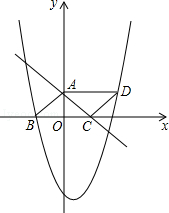
(1)试求b,c的值,并写出该二次函数表达式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:
①当P运动到何处时,有PQ⊥AC?
②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
相关知识点
推荐套卷
如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数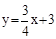 的图象与y轴的交点,点B在二次函数
的图象与y轴的交点,点B在二次函数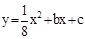 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
(1)试求b,c的值,并写出该二次函数表达式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:
①当P运动到何处时,有PQ⊥AC?
②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?