一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲
地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图像如下图
所示:
(1)根据图像,直接写出y1、y2关于x的函数关系式;
(2)若两车之间的距离为S千米,请写出S关于x的函数关系式;
(3)甲、乙两地间有A、B两个加油站,相距200千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.
相关知识点
推荐套卷
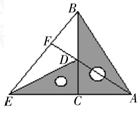
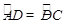 ;②DE⊥AB;③AF=DF.请你写出以①、②、③中的任意两个条件,推出第三个(结论)的一个正确命题.并加以证明.
;②DE⊥AB;③AF=DF.请你写出以①、②、③中的任意两个条件,推出第三个(结论)的一个正确命题.并加以证明.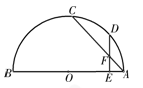
 中,直线AB分别与
中,直线AB分别与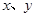 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D,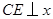 轴于点E,
轴于点E,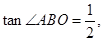
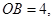
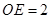 .求该反比例函数的解析式.
.求该反比例函数的解析式.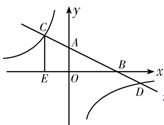
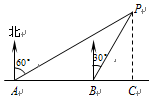
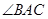 ,
, ,且
,且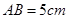 ,求DE的长.
,求DE的长.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号