已知
是由非负整数组成的无穷数列,该数列前
项的最大值记为
,第n项之后各项
,
…的最小值记为
,
.
(1)若
为2,1,4,3,2,1,4,3…,是一个周期为4的数列(即对任意
, ),写出
,
,
,
的值;
),写出
,
,
,
的值;
(2)设d为非负整数,证明:
(
)的充分必要条件为{an}为公差为d的等差数列;
(3)证明:若
,
,则
的项只能是1或2,且有无穷多项为1.
相关知识点
推荐套卷
 ,且
,且 ,
, .
. 、
、 的值;
的值; ,设点
,设点 是函数
是函数 图象上的任意一点,求
图象上的任意一点,求 的最小值,并求此时点
的最小值,并求此时点 的坐标;
的坐标; 时,不等式
时,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 满足
满足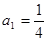 ,
,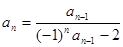 (
(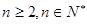 )。
)。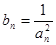 ,求
,求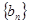 的前n项和
的前n项和 ;
;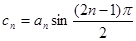 ,数列
,数列 的前n项和
的前n项和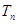 ,求证:对
,求证:对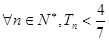 .
.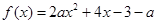 ,
,  .
. 时,求函数
时,求函数 在
在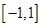 上的最大值;
上的最大值;
 的取值范围.
的取值范围.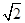 ,E为PD上一点,PE = 2ED.
,E为PD上一点,PE = 2ED.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号