交通管理部门为了优化某路段的交通状况，经过对该路段的长期观测发现：在交通繁忙的时段内，该路段内汽车的车流量
（千辆/时）与汽车的平均速度
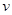（千米/时）之间的函数关系为
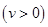
①求在该路段内，当汽车的平均速度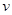为多少时，车流量最大？最大车流量为多少？（精确到
千辆/时）
②若要求在该时段内车流量超过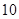
千辆/时，则汽车的平均速度应限定在什么范围内？
中，
，公差为
，其前
项和为
，在等比数列
中，
，公比为
，且
，
．
与
；
满足
，求
的前
．
．
取得最大值时，求自变量
的集合；
的值；
的值．
，且
，求：
及
；
的最小值为
，求实数
的值．
，
，且
，
，求角
的值．推荐套卷
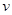交通管理部门为了优化某路段的交通状况，经过对该路段的长期观测发现：在交通繁忙的时段内，该路段内汽车的车流量（千辆/时）与汽车的平均速度（千米/时）之间的函数关系为
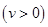
①求在该路段内，当汽车的平均速度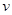为多少时，车流量最大？最大车流量为多少？（精确到千辆/时）
②若要求在该时段内车流量超过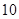千辆/时，则汽车的平均速度应限定在什么范围内？
粤公网安备 44130202000953号