如图，已知椭圆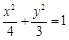
的左焦点为F，过点F的直线交椭圆于A、B两点，线段AB的中点为G，AB的中垂线与x轴和y轴分别交于D、E两点．
（Ⅰ）若点G的横坐标为
，求直线AB的斜率；
（Ⅱ）记△GFD的面积为S1，△OED（O为原点）的面积为S2．
试问：是否存在直线AB，使得S1=S2？说明理由．
； （２）
．
，且
，
的取值范围．
是集合
到
的映射，
，那么映射
是定义在
的函数，满足
．设
，
．当
时，
．分别求当
、
、
时，
、
、
．
的最小值和最大值．推荐套卷
如图，已知椭圆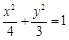的左焦点为F，过点F的直线交椭圆于A、B两点，线段AB的中点为G，AB的中垂线与x轴和y轴分别交于D、E两点．
（Ⅰ）若点G的横坐标为，求直线AB的斜率；
（Ⅱ）记△GFD的面积为S1，△OED（O为原点）的面积为S2．
试问：是否存在直线AB，使得S1=S2？说明理由．
粤公网安备 44130202000953号