如图，在平面直角坐标系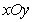
中，以
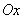轴为始边，两个锐角
,
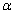的终边分别与单位圆相交于A,B 两点．
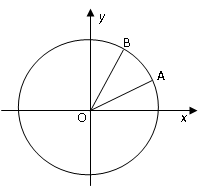
（Ⅰ）若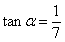
，
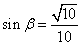，求
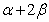的值；
（Ⅱ）若角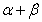
的终边与单位圆交于
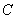点，设角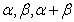
的正弦线分别为
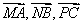，试问：以
作为三边的长能否构成一个三角形？若能，请加以证明；若不能，请说明理由.
作直线
，使它被两相交直线
和
所截得的线段恰好被
点平分，求点
(3，2)发出，经
轴反射，通过点
(－1，6)，求入射光线和反射光线所在的直线方程．
，直线
，
，两平行直线间距离为
，而过点
的直线
被
、
截得的线段长为
，求直线
，且点
到该直线距离等于4，求该直线倾斜角．
经过
，且与点
和
的距离之比为
，求直线相关知识点
推荐套卷
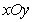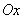如图，在平面直角坐标系中，以轴为始边，两个锐角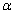,的终边分别与单位圆相交于A,B 两点．
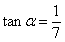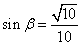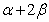（Ⅰ）若，，求的值；
（Ⅱ）若角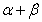的终边与单位圆交于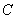点，设角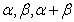的正弦线分别为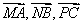，试问：以作为三边的长能否构成一个三角形？若能，请加以证明；若不能，请说明理由.
粤公网安备 44130202000953号