某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.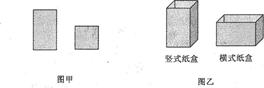
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共l00个,按两种纸盒的生产个数来分,有哪几种生产方案?
(2)若有正方形纸板162张,长方形纸板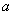 张,做成上述两种纸盒,纸板恰好用完.已知
张,做成上述两种纸盒,纸板恰好用完.已知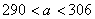 ,求
,求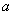 的值.
的值.
相关知识点
推荐套卷
某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共l00个,按两种纸盒的生产个数来分,有哪几种生产方案?
(2)若有正方形纸板162张,长方形纸板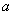 张,做成上述两种纸盒,纸板恰好用完.已知
张,做成上述两种纸盒,纸板恰好用完.已知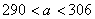 ,求
,求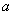 的值.
的值.