小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a>8),就站在A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人.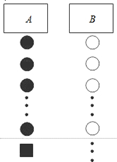
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少?(用含a的代数式表示)
(2)此时,若小杰迅速从A窗口队伍转移到B窗口后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围.(不考虑其它因素)
相关知识点
推荐套卷
 ABC的三个顶点的位置如图所示,点A/的坐标是(-2,2) ,现将
ABC的三个顶点的位置如图所示,点A/的坐标是(-2,2) ,现将
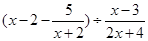 ,其中
,其中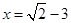 .
.
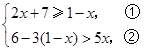 并求出所有整数解的和.
并求出所有整数解的和.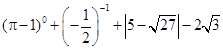 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号