已知二次函数y=－9x2－6ax－a2+2a；(1)当此抛物线经过原点，且对称轴在y轴左侧．
①求此二次函数关系式；(2分)
②设此抛物线与x轴的另一个交点为A,顶点为P，
O为坐标原点．现有一直线l：x=m随着m的
变化从点A向点O平行移动(与点O不重合)，
在运动过程中，直线l与抛物线交于点Q，
求△OPQ的面积S关于m的函数关系式；(5分)
(2)若二次函数在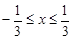
时有最大值－4，求a的值．(5分)
的值，其中
满足：⑴已知
，⑵
是最大的负整数，化简求值：
是四个互不相等的整数，且它们的积
的值；
的方程：
个座位，后面每排都比前一排多
个座位.
排的座位数；
表示第
排的座位数，
时，计算
，其中
.
互为相反数，
互为倒数，
的绝对值为
，求
的值.相关知识点
推荐套卷
已知二次函数y=－9x2－6ax－a2+2a；(1)当此抛物线经过原点，且对称轴在y轴左侧．
①求此二次函数关系式；(2分)
②设此抛物线与x轴的另一个交点为A,顶点为P，
O为坐标原点．现有一直线l：x=m随着m的
变化从点A向点O平行移动(与点O不重合)，
在运动过程中，直线l与抛物线交于点Q，
求△OPQ的面积S关于m的函数关系式；(5分)
(2)若二次函数在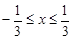时有最大值－4，求a的值．(5分)
粤公网安备 44130202000953号