在某服装批发市场，某种品牌的时装当季节将来临时，价格呈上升趋势，设这种时装开始时定价为20元，并且每周（7天）涨价2元，从第6周开始保持30元的价格平稳销售；从第12周开始，当季节即将过去时，平均每周减价2元，直到第16周周末，该服装不再销售。
⑴试建立销售价y与周次x之间的函数关系式；
⑵若这种时装每件进价Z与周次
次之间的关系为Z＝
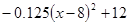,1≤≤16，且为整数，试问该服装第几周出售时，每件销售利润最大？最大利润为多少？
相关试题
的首项
，其前
和为
，且满足
（
N*）．
表示
的值；
，求实数
．
的值；
的最小正周期和单调增区间；
的图像是如何由函数
的图像变换所得．
中，
，且
成等差数列．
，求数列
的前n项和
．
中，设角
的对边分别为
，且
．
的大小；
，
，求边
的大小．
，
.
的单调区间；
时，求
上的最小值，并证明
.推荐套卷
在某服装批发市场，某种品牌的时装当季节将来临时，价格呈上升趋势，设这种时装开始时定价为20元，并且每周（7天）涨价2元，从第6周开始保持30元的价格平稳销售；从第12周开始，当季节即将过去时，平均每周减价2元，直到第16周周末，该服装不再销售。
⑴试建立销售价y与周次x之间的函数关系式；
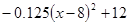⑵若这种时装每件进价Z与周次次之间的关系为Z＝,1≤≤16，且为整数，试问该服装第几周出售时，每件销售利润最大？最大利润为多少？
粤公网安备 44130202000953号