如图,矩形ABCD中,E是AD的中点,EF⊥EC,交AB于点F,连接CF.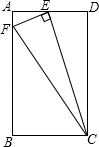
(1)图中的哪些三角形相似?请证明你的判断;
(2)当矩形ABCD满足什么条件时,图中所有的三角形都两两相似?请说明理由.
相关知识点
推荐套卷
如图,矩形ABCD中,E是AD的中点,EF⊥EC,交AB于点F,连接CF.
(1)图中的哪些三角形相似?请证明你的判断;
(2)当矩形ABCD满足什么条件时,图中所有的三角形都两两相似?请说明理由.