已知三个正整数 ,1,
,1, 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求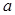 的值;
的值;
(2)若等差数列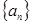 的首项、公差都为
的首项、公差都为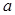 ,等比数列
,等比数列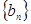 的首项、公比也都为
的首项、公比也都为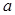 ,前
,前 项和分别
项和分别
为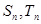 ,且
,且 ,求满足条件的正整数
,求满足条件的正整数 的最大值.
的最大值.
相关知识点
推荐套卷
已知三个正整数 ,1,
,1, 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求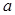 的值;
的值;
(2)若等差数列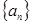 的首项、公差都为
的首项、公差都为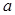 ,等比数列
,等比数列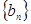 的首项、公比也都为
的首项、公比也都为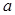 ,前
,前 项和分别
项和分别
为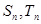 ,且
,且 ,求满足条件的正整数
,求满足条件的正整数 的最大值.
的最大值.