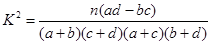为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别
是否需要志愿者
|
男
|
女
|
需要
|
40
|
30
|
不需要
|
160
|
270
|
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有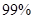 的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中需要志愿者提供帮助的老年人的比例?说明理由.
附:

|
0.050
|
0.010
|
0.001
|

|
3.841
|
6.635
|
10.828
|