(本小题满分14分)
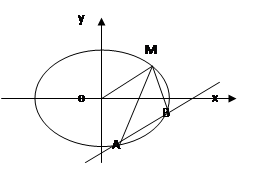
已知椭圆的中心在原点,焦点在 轴上,长轴长是短轴长的2倍,且经过点
轴上,长轴长是短轴长的2倍,且经过点 (2,1),平行于
(2,1),平行于 直线
直线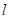 在
在 轴上的截距为
轴上的截距为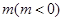 ,设直线
,设直线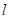 交椭圆于两个不同点
交椭圆于两个不同点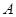 、
、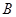 ,
,
(1)求椭圆方程;
(2)求证:对任意的 的允许值,
的允许值, 的内心在定直线
的内心在定直线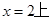 。
。
推荐套卷
(本小题满分14分)
已知椭圆的中心在原点,焦点在 轴上,长轴长是短轴长的2倍,且经过点
轴上,长轴长是短轴长的2倍,且经过点 (2,1),平行于
(2,1),平行于 直线
直线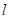 在
在 轴上的截距为
轴上的截距为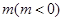 ,设直线
,设直线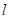 交椭圆于两个不同点
交椭圆于两个不同点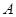 、
、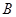 ,
,
(1)求椭圆方程;
(2)求证:对任意的 的允许值,
的允许值, 的内心在定直线
的内心在定直线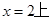 。
。