我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对
该特产的销售投资收益为:每投入x万元,可获得利润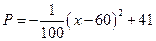 (万元).当
(万元).当
地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项
目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中
拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的
3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,
可获利润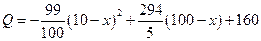 (万元)
(万元)
⑴若不进行开发,求5年所获利润的最大值是多少?
⑵若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
⑶根据⑴、⑵,该方案是否具有实施价值?