(本题满分12分)
为调查某工厂工人生产某种产品的能力，随机抽查了一些工人某天生产产品的数量，产品数量的分组区间为[45,55), [55,65), [65,75), [75,85), [85,95),由此得到频率分布直方图如图所示，保存中不慎丢失一些数据，但已知第一组 （[45,55) ]有4人；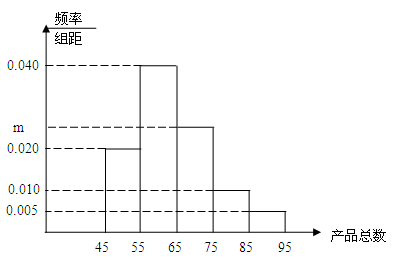
（Ⅰ）求被抽查的工人总人数n及图中所示m为多少；
（Ⅱ）求这些工人中一天生产该产品数量在[55,75)之间的人数是多少。
.
在闭区间
上的最大值是1？若存在，求出对应的a值？若不存在，试说明理由．
，x∈R(其中A＞0，ω＞0,
)的周期为π，且图象上一个最低点为M
.
时，求f(x)的最大值．
，
.
值； (2)求
的值.
.相关知识点
推荐套卷
(本题满分12分)
为调查某工厂工人生产某种产品的能力，随机抽查了一些工人某天生产产品的数量，产品数量的分组区间为[45,55), [55,65), [65,75), [75,85), [85,95),由此得到频率分布直方图如图所示，保存中不慎丢失一些数据，但已知第一组 （[45,55) ]有4人；
（Ⅰ）求被抽查的工人总人数n及图中所示m为多少；
（Ⅱ）求这些工人中一天生产该产品数量在[55,75)之间的人数是多少。
粤公网安备 44130202000953号