（本题满分14分，其中第（1）题4分，第（2）题的第、小题分别为4分、6分）
如图1，在△ABC中，已知AB=15，cosB=
，tanC=
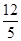．点D为边BC上的动点（点D不与B、C重合），以D为圆心，BD为半径的⊙D交边AB于点E．
（1）设BD=x，AE=y，求
与
的函数关系式，并写出函数定域义；
（2）如图2，点F为边AC上的动点，且满足BD=
CF，联结DF．
①当△ABC和△FDC相似时，求⊙D的半径；
② 当⊙D与以点F为圆心，FC为半径⊙F外切时，求⊙D的半径．
相关试题
＋（－1）2013－（－2）－2．如图，抛物线
的顶点为H，与
轴交于A、B两点（B点在A点右侧），点H、B关于直线：
对称，过点B作直线BK∥AH交直线于K点． 
（1）求A、B两点坐标，并证明点A在直线上；
（2）求此抛物线的解析式；
（3）将此抛物线向上平移，当抛物线经过K点时，设顶点为N，求出NK的长．
如图，△ABC内接于⊙O, AD是⊙O直径, E是CB延长线上一点, 且ÐBAE=ÐC.
（1）求证：直线AE是⊙O的切线；
（2）若EB="AB" , 
, AE=24，求EB的长及⊙O的半径。
，DB="4," 求四边形ABCD的面积．
相关知识点
推荐套卷
粤公网安备 44130202000953号