(10分)如图:一次函数y=-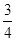 x+6的图象与x轴和y轴分别交于点A和B ,再将△AOB
x+6的图象与x轴和y轴分别交于点A和B ,再将△AOB
沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D。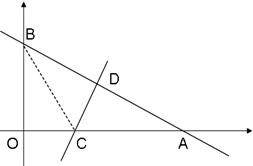
(1)点A的坐标为 ,点B的坐标为 。
(2)求OC的长度 ;
(3)在x轴上有一点P,且△PAB是等腰三角形,不需计算过程,请直接写出点P的坐标 。
相关知识点
推荐套卷
(10分)如图:一次函数y=-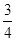 x+6的图象与x轴和y轴分别交于点A和B ,再将△AOB
x+6的图象与x轴和y轴分别交于点A和B ,再将△AOB
沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D。
(1)点A的坐标为 ,点B的坐标为 。
(2)求OC的长度 ;
(3)在x轴上有一点P,且△PAB是等腰三角形,不需计算过程,请直接写出点P的坐标 。