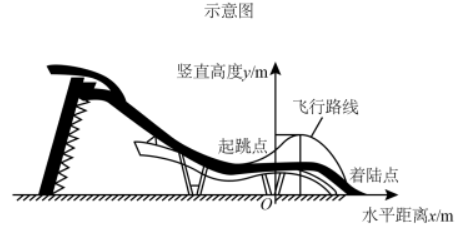
单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台.运动员起跳后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度
(单位:
)与水平距离
(单位:
)近似满足函数关系
.
某运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离
与竖直高度
的几组数据如下:
|
水平距离
|
|
|
|
|
|
|
|
竖直高度
|
|
|
|
|
|
|
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系
;
(2)第二次训练时,该运动员的竖直高度
与水平距离
近似满足函数关系
.记该运动员第一次训练的着陆点的水平距离为
,第二次训练的着陆点的水平距离为
,则
_____
(填“>”“=”或“<”).