已知：一次函数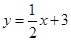
的图象与正比例函数
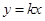的图象相交于点
A（a，1）．
（1）求a的值及正比例函数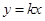的解析式；
（2）点P在坐标轴上（不与点O重合），若PA=OA，直接写出P点的坐标；
（3）直线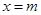
与一次函数的图象交于点B，与正比例函数图象交于点C，若△ABC的面积记为S，求S关于m的函数关系式（写出自变量的取值范围）．
相关试题
在
上，且
，点
是
延长线上一点，
，联结
与
交于点
，求
的值.
中，点
是
边上一点，
，
， 
，
.
∽
；
的值．
的图像经过点
，
，
，求这个二次函数的解析式，并写出点
关于这个二次函数图像的对称轴对称的点
的坐标．
中，
∥
，
的面积等于9，
的面积等于6，
，求
的长.
形的边长为1．位于AD中点处的光点P按图18-2的程序移动
的路径总长（结果保留π）
相关知识点
推荐套卷
已知：一次函数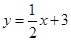的图象与正比例函数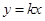的图象相交于点
A（a，1）．
（1）求a的值及正比例函数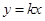的解析式；
（2）点P在坐标轴上（不与点O重合），若PA=OA，直接写出P点的坐标；
（3）直线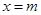与一次函数的图象交于点B，与正比例函数图象交于点C，若△ABC的面积记为S，求S关于m的函数关系式（写出自变量的取值范围）．
粤公网安备 44130202000953号