(14分)如图，在三棱锥S—ABC中，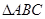
是边长为4的正三角形，平面SAC⊥平面ABC，SA =" SC" =
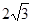，M、N分别为AB、SB的中点。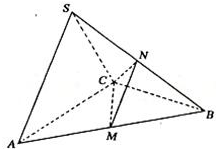
⑴ 求证：AC⊥SB；
⑵ 求二面角N—CM—B的正切值；
⑶ 求点B到平面CMN的距离。
在区间[－1,1]上单调递增，求
的取值范围.
是
上的可导函数，若
在
时恒成立.
在
时，有
.
在
处取得极值，其图象在
处的切线的斜率为
。求证：
；
，
．令
，讨论
在
内的单调性并求极值；
，其中
。设两曲线
有公共点，且在公共点处的切线相同。
，求
的值；
表示推荐套卷
(14分)如图，在三棱锥S—ABC中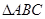，是边长为4的正三角形，平面SAC⊥平面ABC，SA =" SC" =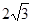，M、N分别为AB、SB的中点。
⑴ 求证：AC⊥SB；
⑵ 求二面角N—CM—B的正切值；
⑶ 求点B到平面CMN的距离。
粤公网安备 44130202000953号