（本小题满分12分）
如图：四棱锥P-ABCD中，底面ABCD是平行四边形，∠ACB＝90°，平面PAD⊥平面ABCD，PA=BC=1，PD=AB=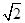
,E、F分别为线段PD和BC的中点．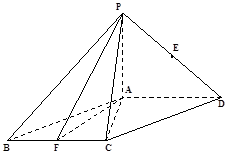
(Ⅰ) 求证：CE∥平面PAF；
(Ⅱ) 在线段BC上是否存在一点G，使得平面PAG和平面PGC所成二面角的大小为60°？若存在，试确定G的位置；若不存在，请说明理由．
，对于满足
的一切
值都有
，求实数
的取值范围。
的值域；
，求
的值。
，且
。
的最大值，并求出相应的
、
的值。
一个周期的图象如图所示。 
的表达式；
，且A为△ABC的一个内角，求：
的值。
=1，
=2，
与
的夹角为60°。
，（
）·（
）；（2）求：
。推荐套卷
（本小题满分12分）
如图：四棱锥P-ABCD中，底面ABCD是平行四边形，∠ACB＝90°，平面PAD⊥平面ABCD，PA=BC=1，PD=AB=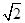,E、F分别为线段PD和BC的中点．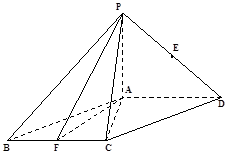
(Ⅰ) 求证：CE∥平面PAF；
(Ⅱ) 在线段BC上是否存在一点G，使得平面PAG和平面PGC所成二面角的大小为60°？若存在，试确定G的位置；若不存在，请说明理由．
粤公网安备 44130202000953号