如图，已知抛物线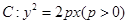
上横坐标为4的点到焦点的距离为5．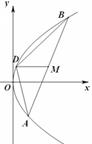
（Ⅰ）求抛物线C的方程；
（Ⅱ）设直线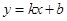
与抛物线C交于两点
，
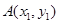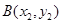，且
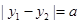（a为正常数）．过弦AB的中点M作平行于x轴的直线交抛物线C于点D，连结AD、BD得到
．
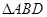（i）求实数a，b，k满足的等量关系；
（ii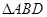）的面积是否为定值？若为定值，求出此定值；若不是定值，请说明理由．
相关试题
.
的单调区间；
，求
上的最大值；
，不等式
恒成立．
，
．
在
上的值域；
2）若对于任意
，总存在
，使得
成立，求
的取值范围．
，若
图象上的点
处的切线斜率为
，求
上的最值.
12分）
(
），比较
、
、
的大小，并证明你的结论
，函数
的两个零点为
.
求不等式
的解集；
且
，比较
与
的大小．推荐套卷
如图，已知抛物线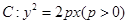上横坐标为4的点到焦点的距离为5．
（Ⅰ）求抛物线C的方程；
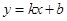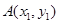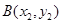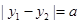（Ⅱ）设直线与抛物线C交于两点，，且（a为正常数）．过弦AB的中点M作平行于x轴的直线交抛物线C于点D，连结AD、BD得到．
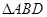（i）求实数a，b，k满足的等量关系；
（ii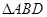）的面积是否为定值？若为定值，求出此定值；若不是定值，请说明理由．
粤公网安备 44130202000953号