如图,△ABC的顶点在格点上,且点A(-5,-1),点C(-1,-2).
(1)以原点O为旋转中心,将△ABC绕点O逆时针旋转90°得到△ . 请在图中画出△
. 请在图中画出△ ,并写出点A的对称点
,并写出点A的对称点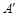 的坐标;
的坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的图形△ .
.
相关知识点
推荐套卷
如图,△ABC的顶点在格点上,且点A(-5,-1),点C(-1,-2).
(1)以原点O为旋转中心,将△ABC绕点O逆时针旋转90°得到△ . 请在图中画出△
. 请在图中画出△ ,并写出点A的对称点
,并写出点A的对称点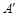 的坐标;
的坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的图形△ .
.