如图，设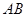
、
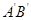分别是圆
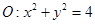和椭圆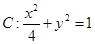
的弦，且弦的端点在
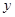轴的异侧，端点
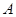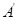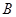与
、
与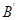
的横坐标分别相等，纵坐标分别同号.
（Ⅰ）若弦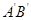所在直线斜率为
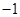，且弦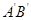的中点的横坐标为
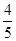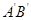，求直线的方程；
（Ⅱ）若弦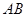过定点
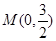，试探究弦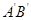是否也必过某个定点. 若有，请证明；若没有，请说明理由.
相关试题
中，
底面
， 
．底面
，
.
，点
在棱
上，且
．
平面
；
的大小．
的方程为
.
的圆
作直线与圆
两点，求
的最大面积以及此时直线
的斜率.
的展开式中前三项的系数成等差数列．
（2）求展开式中系数最大的项．
(
)和
(
)，
．
的最大值；（2）若
，求
的值
．
？
，存在不平行于x轴的直线l与椭圆交于不同两点M、N，使推荐套卷
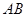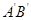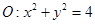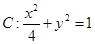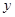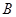如图，设、分别是圆和椭圆的弦，且弦的端点在轴的异侧，端点与、与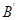的横坐标分别相等，纵坐标分别同号.
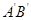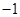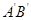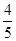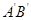（Ⅰ）若弦所在直线斜率为，且弦的中点的横坐标为，求直线的方程；
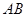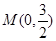（Ⅱ）若弦过定点，试探究弦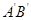是否也必过某个定点. 若有，请证明；若没有，请说明理由.
粤公网安备 44130202000953号