岳阳市一中高三有五个文科平行班。湖南省高三数学适应性测试后,随机地在各班抽取
了部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班
被抽取了 人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如下图所示,
人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如下图所示,
其中 (包括
(包括 分但不包括
分但不包括 分)的频率为
分)的频率为 ,此分数段的人数为
,此分数段的人数为 人.
人.  (1)问各班被抽取的学生人数分别是多少人?
(1)问各班被抽取的学生人数分别是多少人?
(2)在抽取的所有学生中,任取一名学生,
求分数不小于 分的概率。
分的概率。
相关知识点
推荐套卷
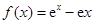 .
. 的最小值;
的最小值;
 ;
; 与
与 定义域上的任意实数
定义域上的任意实数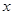 ,若存在常数
,若存在常数 ,使得
,使得 和
和 都成立,则称直线
都成立,则称直线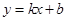 为函数
为函数 ,
, ,
,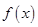 对任意
对任意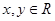 ,都有
,都有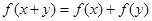 ,当
,当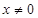 时,
时,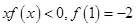
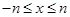 时
时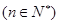 ,
,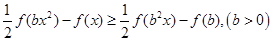
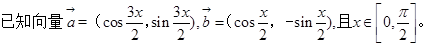
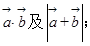
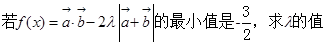 .
.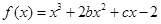 的图象在与
的图象在与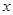 轴交点处的切线方程是
轴交点处的切线方程是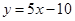 .
.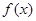 的解析式;
的解析式;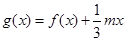 ,若
,若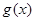 的极值存在,求实数
的极值存在,求实数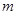 的取值范围以及函数
的取值范围以及函数 粤公网安备 44130202000953号
粤公网安备 44130202000953号