如图,有一边长为2米的正方形钢板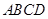 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线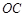 是以直线
是以直线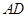 为对称轴,以线段
为对称轴,以线段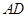 的中点
的中点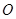 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
(Ⅰ)请建立适当的直角坐标系,求阴影部分的边缘线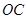 的方程;
的方程;
(Ⅱ)如何画出切割路径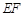 ,使得剩余部分即直角梯形
,使得剩余部分即直角梯形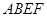 的面积最大?
的面积最大?
并求其最大值.
推荐套卷
如图,有一边长为2米的正方形钢板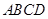 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线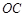 是以直线
是以直线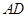 为对称轴,以线段
为对称轴,以线段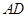 的中点
的中点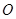 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
(Ⅰ)请建立适当的直角坐标系,求阴影部分的边缘线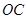 的方程;
的方程;
(Ⅱ)如何画出切割路径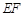 ,使得剩余部分即直角梯形
,使得剩余部分即直角梯形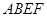 的面积最大?
的面积最大?
并求其最大值.