作出函数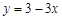 的图象,并根据图象回答下列问题:
的图象,并根据图象回答下列问题:
(1)y的值随x的增大而 ;
(2)图象与x轴的交点坐标是 ;与y轴的交点坐标是 ;
(3)当x 时,y≥0;
(4)函数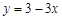 的图象与坐标轴所围成的三角形的面积是________________。
的图象与坐标轴所围成的三角形的面积是________________。
相关知识点
推荐套卷
作出函数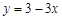 的图象,并根据图象回答下列问题:
的图象,并根据图象回答下列问题:
(1)y的值随x的增大而 ;
(2)图象与x轴的交点坐标是 ;与y轴的交点坐标是 ;
(3)当x 时,y≥0;
(4)函数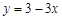 的图象与坐标轴所围成的三角形的面积是________________。
的图象与坐标轴所围成的三角形的面积是________________。