如图1,已知三角形ABC中,AB=BC=1,∠ABC=90度,把一块含30度角的三角板DEF的直角顶点D放在AC的中点上,将直角三角板DEF绕D点按逆时针方向旋转。
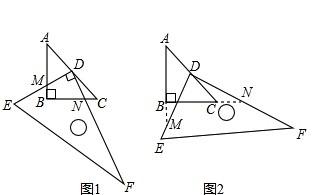
(1)在图1中,DE交AB于M,DF交BC于N.
①直接写出DM、DN的数量关系;
②在这一过程中,直角三角板DEF与三角形ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明如何变化的;若不发生变化,请求出其面积.
(2)继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由.