如图：△ABC的三个内角∠A、∠B、∠C所对的边长分别为a、b、c，且满足关系：a2+b2=c2.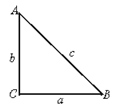
请作一个三角形A′B′C′,使∠C′=90°,B′C′=a,A′C′=b.
（1）△A′B′C′是否全等于△ABC？为什么？
（2）∠C′是否等于∠C？
（3）由以上你能判定△ABC是直角三角形吗？请你想一想，三角形三条边长满足什么关系，这个三角形一定是直角三角形？
相关试题
如图：△ABC的三个内角∠A、∠B、∠C所对的边长分别为a、b、c，且满足关系：a2+b2=c2.
请作一个三角形A′B′C′,使∠C′=90°,B′C′=a,A′C′=b.
（1）△A′B′C′是否全等于△ABC？为什么？
（2）∠C′是否等于∠C？
（3）由以上你能判定△ABC是直角三角形吗？请你想一想，三角形三条边长满足什么关系，这个三角形一定是直角三角形？
位置：
，则点P在. 
，则点P 在 .
，则P在 .
粤公网安备 44130202000953号