(本题满分12分)在直角坐标系xOy中，直线l的参数方程为：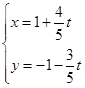
(t为参数)，若以O为极点，x轴正半轴为极轴建立极坐标系，则曲线C的极坐标方程为r=
cos(θ+
)，求直线l被曲线C所截的弦长．
相关试题
中，
的对边分别为
，向量
，
．
，求满足
的角
的值；
，试用角
与
；
，且
的值．
（1）求边AB的值；（2）求sin(B－C)的值。
中，
，
是
上的一个动点，
最小时，求
的值。
时，求相关知识点
推荐套卷
(本题满分12分)在直角坐标系xOy中，直线l的参数方程为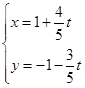：(t为参数)，若以O为极点，x轴正半轴为极轴建立极坐标系，则曲线C的极坐标方程为r=cos(θ+)，求直线l被曲线C所截的弦长．
粤公网安备 44130202000953号