(本题10分)已知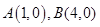 ,动点
,动点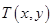 满足
满足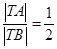 ,设动点
,设动点 的轨迹是曲线
的轨迹是曲线 ,直线
,直线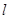 :
: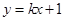 与曲线
与曲线 交于
交于 两点.(1)求曲线
两点.(1)求曲线 的方程;
的方程;
(2)若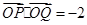 ,求实数
,求实数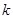 的值;
的值;
(3)过点 作直线
作直线 与
与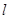 垂直,且直线
垂直,且直线 与曲线
与曲线 交于
交于 两点,求四边形
两点,求四边形 面积的最大值.
面积的最大值.
推荐套卷
(本题10分)已知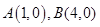 ,动点
,动点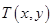 满足
满足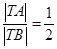 ,设动点
,设动点 的轨迹是曲线
的轨迹是曲线 ,直线
,直线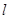 :
: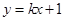 与曲线
与曲线 交于
交于 两点.(1)求曲线
两点.(1)求曲线 的方程;
的方程;
(2)若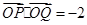 ,求实数
,求实数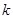 的值;
的值;
(3)过点 作直线
作直线 与
与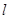 垂直,且直线
垂直,且直线 与曲线
与曲线 交于
交于 两点,求四边形
两点,求四边形 面积的最大值.
面积的最大值.