(本小题11分)如图,三棱锥C—ABD,CB = CD,AB = AD,∠BAD = 90°。E、F分别是BC、AC的中点。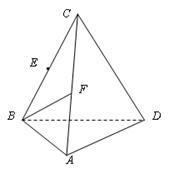
(1)求证:AC⊥BD;
(2)若CA = CB,求证:平面BCD⊥平面ABD
(3)在 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出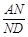 的值
的值
推荐套卷
(本小题11分)如图,三棱锥C—ABD,CB = CD,AB = AD,∠BAD = 90°。E、F分别是BC、AC的中点。
(1)求证:AC⊥BD;
(2)若CA = CB,求证:平面BCD⊥平面ABD
(3)在 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出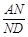 的值
的值