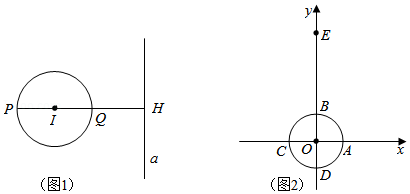如图1,
与直线
相离,过圆心
作直线
的垂线,垂足为
,且交
于
、
两点
在
、
之间).我们把点
称为
关于直线
的“远点“,把
的值称为
关于直线
的“特征数”.
(1)如图2,在平面直角坐标系
中,点
的坐标为
.半径为1的
与两坐标轴交于点
、
、
、
.
①过点
画垂直于
轴的直线
,则
关于直线
的“远点”是点 (填“
”.“
”、“
”或“
”
,
关于直线
的“特征数”为 ;
②若直线
的函数表达式为
.求
关于直线
的“特征数”;
(2)在平面直角坐标系
中,直线
经过点
,点
是坐标平面内一点,以
为圆心,
为半径作
.若
与直线
相离,点
是
关于直线
的“远点”.且
关于直线
的“特征数”是
,求直线
的函数表达式.