2013年全国第十二届全运会由沈阳承办。城建部门计划在浑南新区建造一个长方形公园ABCD，公园由长方形的休闲区A1B1C1D1（阴影部分）和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米，人行道的宽分别为4米和10米。
（1）若设休闲区的长
米，求公园ABCD所占面积S关于
的函数
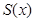的解析式；
（2）要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？
的不等式 
，
的前
项和为
，且 
．
，数列
的前
，求证：
．
的最大值
中，点
是
的中点，点
在
上，且
，
与
交于点
，求
与
的值。
．
的大小；
，
边上的中线
的长为
，求
的面积．推荐套卷
2013年全国第十二届全运会由沈阳承办。城建部门计划在浑南新区建造一个长方形公园ABCD，公园由长方形的休闲区A1B1C1D1（阴影部分）和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米，人行道的宽分别为4米和10米。
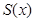（1）若设休闲区的长米，求公园ABCD所占面积S关于的函数的解析式；
（2）要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？
粤公网安备 44130202000953号