有一个湖泊受污染，其湖水的容量为V立方米，每天流入湖的水量等于流出湖的水量. 现假设下雨和蒸发平衡，且污染物和湖水均匀混合.
用
，表示某一时刻一立方米湖水中所含污染物的克数（我们称其湖水污染质量分数），
表示湖水污染初始质量分数.
（1）当湖水污染质量分数为常数时，求湖水污染初始质量分数；
（2）分析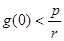
时，湖水的污染程度如何.
，求x的范围；
的最大值以及此时x的值.
在
时取得最大值4．
的最小正周期；
,求
为锐角，求
的范围；
时，求
的值；
的值.
；
时，求
的值.推荐套卷
有一个湖泊受污染，其湖水的容量为V立方米，每天流入湖的水量等于流出湖的水量. 现假设下雨和蒸发平衡，且污染物和湖水均匀混合.
用，表示某一时刻一立方米湖水中所含污染物的克数（我们称其湖水污染质量分数），表示湖水污染初始质量分数.
（1）当湖水污染质量分数为常数时，求湖水污染初始质量分数；
（2）分析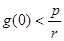时，湖水的污染程度如何.
粤公网安备 44130202000953号