已知直线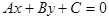
，
（1）系数为什么值时，方程表示通过原点的直线；
（2）系数满足什么关系时与坐标轴都相交；
（3）系数满足什么条件时只与x轴相交；
（4）系数满足什么条件时是x轴；
（5）设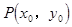
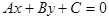为直线上一点，
证明：这条直线的方程可以写成
．
的值．
，当
时，有
，
的值，使
与
都是有限的．推荐套卷
已知直线，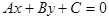
（1）系数为什么值时，方程表示通过原点的直线；
（2）系数满足什么关系时与坐标轴都相交；
（3）系数满足什么条件时只与x轴相交；
（4）系数满足什么条件时是x轴；
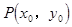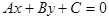（5）设为直线上一点，
证明：这条直线的方程可以写成．
粤公网安备 44130202000953号