(本小题12分)
某市居民生活用水收费标准如下:
用水量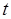 (吨) (吨) |
每吨收费标准(元) |
不超过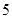 吨部分 吨部分 |
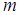 |
超过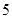 吨不超过 吨不超过 吨部分 吨部分 |
3 |
超过 吨部分 吨部分 |
 |
已知某用户一月份用水量为 吨,缴纳的水费为
吨,缴纳的水费为 元;二月份用水量为
元;二月份用水量为 吨,缴纳的水费为
吨,缴纳的水费为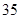 元.设某用户月用水量为
元.设某用户月用水量为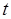 吨,交纳的水费为
吨,交纳的水费为 元.
元.
(1)写出 关于
关于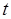 的函数关系式;
的函数关系式;
(2)若某用户希望三月份缴纳的水费不超过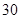 元,求该用户三月份最多可以用多少吨水?
元,求该用户三月份最多可以用多少吨水?
推荐套卷
(本小题12分)
某市居民生活用水收费标准如下:
用水量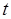 (吨) (吨) |
每吨收费标准(元) |
不超过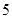 吨部分 吨部分 |
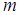 |
超过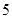 吨不超过 吨不超过 吨部分 吨部分 |
3 |
超过 吨部分 吨部分 |
 |
已知某用户一月份用水量为 吨,缴纳的水费为
吨,缴纳的水费为 元;二月份用水量为
元;二月份用水量为 吨,缴纳的水费为
吨,缴纳的水费为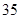 元.设某用户月用水量为
元.设某用户月用水量为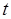 吨,交纳的水费为
吨,交纳的水费为 元.
元.
(1)写出 关于
关于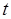 的函数关系式;
的函数关系式;
(2)若某用户希望三月份缴纳的水费不超过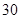 元,求该用户三月份最多可以用多少吨水?
元,求该用户三月份最多可以用多少吨水?