(本小题满分14分)
平面直角坐标系中,已知直线 :
: ,定点
,定点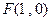 ,动点
,动点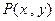 到直线
到直线 的距离是到定点
的距离是到定点 的距离的2倍.
的距离的2倍.
(1)求动点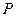 的轨迹
的轨迹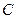 的方程;
的方程;
(2)若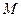 为轨迹
为轨迹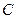 上的点,以
上的点,以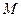 为圆心,
为圆心,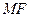 长为半径作圆
长为半径作圆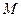 ,若过点
,若过点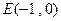 可作圆
可作圆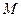 的两条切线
的两条切线 ,
, (
( ,
,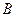 为切点),求四边形
为切点),求四边形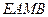 面积的最大值.
面积的最大值.
推荐套卷
(本小题满分14分)
平面直角坐标系中,已知直线 :
: ,定点
,定点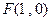 ,动点
,动点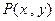 到直线
到直线 的距离是到定点
的距离是到定点 的距离的2倍.
的距离的2倍.
(1)求动点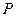 的轨迹
的轨迹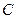 的方程;
的方程;
(2)若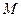 为轨迹
为轨迹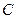 上的点,以
上的点,以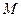 为圆心,
为圆心,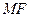 长为半径作圆
长为半径作圆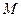 ,若过点
,若过点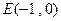 可作圆
可作圆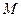 的两条切线
的两条切线 ,
, (
( ,
,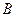 为切点),求四边形
为切点),求四边形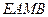 面积的最大值.
面积的最大值.