如图，在□ ABCD中，BD为对角线，EF垂直平分BD分别交AD、BC的于点E、F，交BD于点O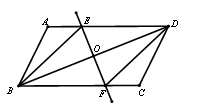
(1)试说明：BF＝DE；
(2)试说明：△ABE≌△CDF；
(3)如果在□ ABCD中， AB＝5，AD＝10，有两动点P、Q分别从B、D两点同时出发,沿△BAE和△DFC各边运动一周，即点
自B→A→E→B停止，点Q自D→F→C→D停止，点P运动的路程是m，点Q运动的路程是n，当四边形BPDQ是平行四边形时，求m与n满足的数量关系．(画出示意图)
相关试题
甲、乙两位运动员进行射击比赛，各射击了10次，每次命中环数如下：
甲：8，6，7，8，9，10，6，5，4，7
乙：7，9，8，5，6，7， 7，6，7，8
（1）甲、乙运动员的平均成绩分别是多少？
（2）这十次比赛成绩的方差分别是多少？
（3）试分析这两名运动员的射击成绩.
（注：方差公式
6分）已知一次函数
，完成下列问题：
|
（1）画出函数图象.
（2）直接写出图象与x轴、y轴的交点A、B的坐标.（3）观察图象，写出x在什么范围内取值时，y>0.
的顶点A（-4，5），B（-2，1），完成下列问题：
的坐标
，使
.（注：点C必须在格点上） 
，
.求代数式
的值.相关知识点
推荐套卷
粤公网安备 44130202000953号