如图，渔船甲位于岛屿
的南偏西
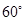方向的
处，且与岛屿相距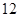
海里，渔船乙以
海里/ 小时的速度从岛屿出发沿正北方向航行，若渔船甲同时从处出发沿北偏东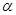
的方向追赶渔船乙，刚好用
小时追上.
（1）求渔船甲的速度；
（2）求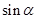
的值. 
的方程为
．
的取值范围．
在两坐标轴上的截距相等，且
到直线
，求直线
垂直，且在
轴上的截距比在
轴上的截距大2的直线方程．
且与两坐标轴围成三角形的周长是12的直线
的方程．
中，侧面
与面
垂直，
．
；
，求
与平面
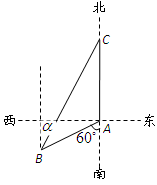
所成角的大小．相关知识点
推荐套卷
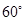如图，渔船甲位于岛屿的南偏西方向的处，且与岛屿相距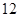海里，渔船乙以海里/ 小时的速度从岛屿出发沿正北方向航行，若渔船甲同时从处出发沿北偏东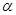的方向追赶渔船乙，刚好用小时追上.
（1）求渔船甲的速度；
（2）求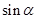的值.
粤公网安备 44130202000953号