如图，已知椭圆C：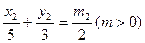
，经过椭圆C的右焦点F且斜率为k（k≠0）的直线l交椭圆G于A、B两点，M为线段AB的中点，设O为椭圆的中心，射线OM交椭圆于N点．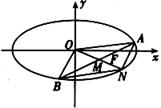
（1）是否存在k，使对任意m＞0，总有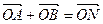
成立？若存在，求出所有k的值；
（2）若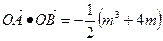
，求实数k的取值范围．
；
，其中
的顶点
，
边上的中线
所在的直线方程为
，
边上的高
所在直线方程为
．
的坐标；
的方程．
经过点
和直线
相切，且圆心在直线
上，求圆
和
的交点，且垂直于直线
的直线方程．
，求值：
推荐套卷
如图，已知椭圆C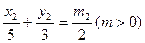：，经过椭圆C的右焦点F且斜率为k（k≠0）的直线l交椭圆G于A、B两点，M为线段AB的中点，设O为椭圆的中心，射线OM交椭圆于N点．
（1）是否存在k，使对任意m＞0，总有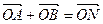成立？若存在，求出所有k的值；
（2）若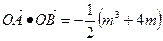，求实数k的取值范围．
粤公网安备 44130202000953号