（本小题满分14分）（注意：仙中、一中、八中的学生三问全做，其他学校的学生只做前两问）
已知函数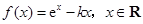
（Ⅰ）若
，试确定函数
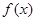的单调区间；
（Ⅱ）若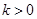
，且对于任意
，
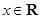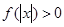恒成立，试确定实数
的取值范围；
（Ⅲ）设函数
，求证：
．
相关试题
是实数，且
；
的实部和虚部都是整数．
，且
为纯虚数，求
的最大值及当
取最大值时的
．
的两个顶点
对应的复数分别为
、
．求另外两个顶点
对应的复数．
取何值时，复数
的方程
有实数根
．
，
满足
，求
有最小值并求出最小值．推荐套卷
（本小题满分14分）（注意：仙中、一中、八中的学生三问全做，其他学校的学生只做前两问）
已知函数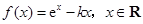
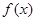（Ⅰ）若，试确定函数的单调区间；
（Ⅱ）若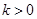，且对于任意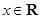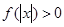，恒成立，试确定实数的取值范围；
（Ⅲ）设函数，求证：．
粤公网安备 44130202000953号