如图甲,在直角坐标系中,点A,B的坐标分别为(0,2)、(2,2).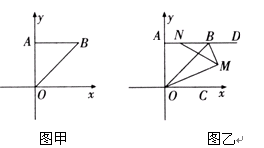
(1)求△AOB的面积;
(2)如图乙,点D为AB延长线上一点,点C为x轴正半轴上一点,分别作∠DBO与∠BOC的平分线交于点M,点N为AB上一点,求∠BNM+∠BMN+∠MOC的度数.
相关知识点
推荐套卷
如图甲,在直角坐标系中,点A,B的坐标分别为(0,2)、(2,2).
(1)求△AOB的面积;
(2)如图乙,点D为AB延长线上一点,点C为x轴正半轴上一点,分别作∠DBO与∠BOC的平分线交于点M,点N为AB上一点,求∠BNM+∠BMN+∠MOC的度数.