某工厂生产A产品x吨所需费用为P元,而卖出x吨这种产品的售价为每吨Q元, 已知P=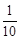 x2+5x+1000,Q=-
x2+5x+1000,Q=- +45.
+45.
(1)该厂生产并售出x吨,写出这种产品所获利润W(元)关于x(吨)的函数关系式;
(2)当生产多少吨这种产品,并全部售出时,获利最多?这时获利多少元? 这时每吨的价格又是多少元?
某工厂生产A产品x吨所需费用为P元,而卖出x吨这种产品的售价为每吨Q元, 已知P=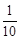 x2+5x+1000,Q=-
x2+5x+1000,Q=- +45.
+45.
(1)该厂生产并售出x吨,写出这种产品所获利润W(元)关于x(吨)的函数关系式;
(2)当生产多少吨这种产品,并全部售出时,获利最多?这时获利多少元? 这时每吨的价格又是多少元?