如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.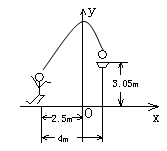
(1)建立如图所示的直角坐标系,求抛物线所对应的函数关系式;
(2)若该运动员身高1.8m,这次跳投时,球在他头顶上方0.25m处出手.问:球出手时,他跳离地面多高?
相关试题
如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.
(1)建立如图所示的直角坐标系,求抛物线所对应的函数关系式;
(2)若该运动员身高1.8m,这次跳投时,球在他头顶上方0.25m处出手.问:球出手时,他跳离地面多高?
中，
，
，且
，E是PC的中点．
；
；
是
的内角，
分别是其对边长，向量
，
，
.
求
的长.
是分别从集合A={1，2，3，4}中随机抽取的元素，集合B=
的所有实数对
与
的值满足
的概率.
的函数
是奇函数
的解析式；
，不等式
恒成立，求
的取值范围.
为偶函数，且在区间
上是单调递减函数，
的解析式；
的奇偶性。
粤公网安备 44130202000953号