某气球内充满了一定质量的气球，当温度不变时，气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数，其图象如图所示(千帕是一种压强单位)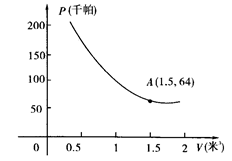
（1）写出这个函数的解析式；
（2）当气球的体积为0.8立方米时，气球内的气压是多少千帕；
（3）当气球内的气压大于144千帕时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米。
相关试题
甲、乙两人共同解方程组
，由于甲错了方程①中的a，得到方程组的解为
；乙看错了方程②中的b，得到方程组的解为
，
(1)求出a，b的值；
(2)求2a﹣3b+5的立方根；
(3)此方程组正确的解应该是多少?
如图，有一块不规则的四边形图形ABCD，各个顶点的坐标分别为A（﹣2，8），B（﹣11，6），C（﹣14，0），D（0，0），
（1）确定这个四边形的面积
（2）如果把原来四边形ABCD的各个顶点的纵坐标保持不变，横坐标加1，画出平移后的图形。
（3）求出平移后四边形面积
的值．完成证明：（1）如图1，已知直线b∥c，a⊥c，求证：a⊥b
证明：∵a⊥c
∴∠1=________
∵b∥c
∴∠1=∠2 （ ）
∴∠2=∠1=90°
∴a⊥b ；
（2）如图2：AB∥CD，∠B+∠D=180°，求证：CB∥DE
证明：∵AB∥CD （已知）
∴∠B=________（ ）
∵∠B+∠D="180°" （已知）
∴∠C+∠D="180°" （ ）
∴CB∥DE （ ）
粤公网安备 44130202000953号