如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数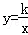
（k≠0）在第一象限内的图象经过点D、E，且tan∠BOA=
．
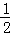（1）求边AB的长；
（2）求反比例函数的解析式和n的值；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．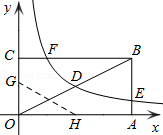
相关试题
－1＝
|×(－10)2
－[10
]
相关知识点
推荐套卷
如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数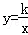（k≠0）在第一象限内的图象经过点D、E，且tan∠BOA=．
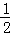（1）求边AB的长；
（2）求反比例函数的解析式和n的值；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．
粤公网安备 44130202000953号