把下列各数分别填在表示它所在的集合里:
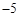 ,
,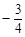 ,0,
,0,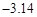 ,
,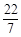 ,2012,1.99,
,2012,1.99,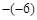 ,
,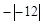
(1)正数集合:{ };
(2)负数集合:{ };
(3)整数集合:{ };
(4)分数集合:{ }。
相关知识点
推荐套卷
把下列各数分别填在表示它所在的集合里:
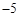 ,
,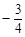 ,0,
,0,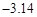 ,
,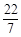 ,2012,1.99,
,2012,1.99,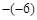 ,
,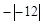
(1)正数集合:{ };
(2)负数集合:{ };
(3)整数集合:{ };
(4)分数集合:{ }。